Bernoulli-Experimente
Wird ein Zufallsexperiment durchgeführt, bei dem als Ergebnis nur "Treffer" oder "kein Treffer" herauskommen kann,
so nennt man dieses ein Bernoulli-Experiment.
Führt man dasselbe Bernoulli-Experiment n mal hintereinander aus, so hat man eine Bernoulli-Kette der Länge n.
Wir führen die Zufallsvariable X ein, welche die Anzahl der Treffer in einer Bernoulli-Kette der Länge n beschreibt.
Ist die Wahrscheinlichkeit p eines einzelnen Treffers bekannt, so kann man nach der Wahrscheinlichkeit fragen,
dass eine bestimmte Trefferanzahl k vorliegt. Formal P(X=k)=?.
Berechnung von P(X=k)
Die Trefferwahrscheinlichkeit eines einzelnen Treffers sei p (wie oben).
Die Wahrscheinlichkeit, dass in einer Bernoulli-Kette der Länge n k Treffer erzielt werden ist gegeben durch den Ausdruck
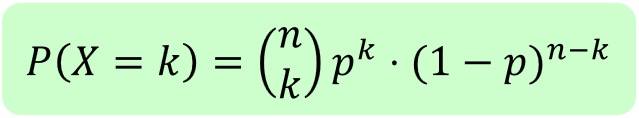
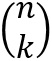(gelesen "n über k") der so genannte Binomialkoeffizient, welchen man mit dem
GTR über MATH PRB nCr bestimmen kann.Beispiel:
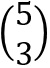gibt man im GTR so ein: 5 MATH PRB nCr 3 ENTER. Das Ergebnis ist 10.Erläuterung der Formel
Eine Münze soll 7mal hintereinander geworfen werden. Wie groß ist die Wahrscheinlichkeit dafür, dass wir 3mal Zahl erhalten?
Lösung
Die WS für Zahl (in einem Wurf) ist p=1/2.
Die WS für Kopf (in einem Wurf) ist 1-p=1/2.
Wir dürfen nicht vergessen, dass bei 7maligem Werfen und 3mal Zahl, zwangsläufig 7-3=4mal Kopf erscheint!
Die WS für 3mal Zahl und 4mal Kopf ist p3·(1-p)4=(1/2)3·(1/2)4
Nun können 3mal Zahl und 4mal Kopf aber auf verschiedene Arten eintreten, z.B. so
Wie viele solcher Verteilungen gibt es?
Dies lässt sich durch den Ausdruck
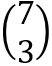(gelesen 7 über 3) bestimmen. Oben steht die Anzahl der Würfe, unten die Anzahl der Treffer (7 Würfe, 3mal Zahl).Insgesamt lautet die Formel für die WS von 3mal Zahl in 7 Würfen also:
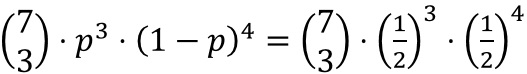
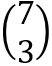berechnen wir mit dem GTR durch Eingabe von 7 MATH PRB nCr 3 ENTER. Wir erhalten den Wert 35.Wenn wir mit der Zufallsvariablen X die "Anzahl Zahl" beschreiben, können wir jetzt formal schreiben:
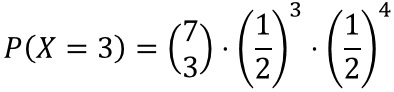
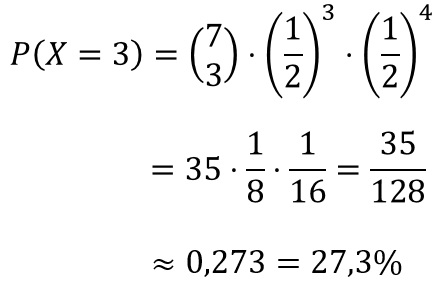
Bei einem Würfelexperiment fragen wir nach der Wahrscheinlichkeit einer 3.
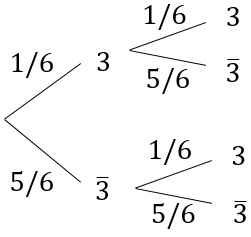Somit gibt es zwei mögliche Ausgänge, nämlich eine 3 (Treffer) oder keine 3 (kein Treffer).Das Experiment wird zweimal wiederholt und die Anzahl der der Treffer notiert.
Die Zufallsvariable X beschreibt die Anzahl der Treffer.
Dann kann X die Werte 0, 1 oder 2 annehmen und es gilt:
P(X=0) = (5/6)2 ≈ 69,44%
P(X=1) = 2·(1/6)·(5/6) ≈ 27,78%
P(X=2) = (1/6)2 ≈ 2,78%
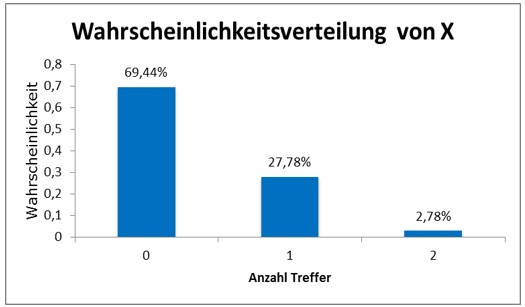
Die Wahrscheinlichkeiten für die verschiedenen Trefferanzahlen können wir wieder als Histogramm darstellen und erhalten so die eine Veranschaulichung der Wahrscheinlichkeitsverteilung von X.
| Downloads |
PowerPoint